LSTM

#DL基础 2025-04-06

目录

1. LSTM
   1. LSTM 结构
      1. 一些参数
      2. 四个门控制机制
   2. 代码演示
   3. LSTM 反向传播的优势
      1. 梯度流
      2. LSTM 如何用元素乘法解决梯度问题
   4. LSTM 和ResNet 的相似性
   5. RNN 可解释性研究
      1. 背景 : RNN 内部工作机制难以解释
      2. 实验设计
      3. 三组比较
      4. LSTM 内部原理可视化
         1. 可解释的长距离 LSTM 单元 (Interpretable, long-range LSTM cells)
         2. 门控激活统计分析(Gate Activation Statistics)
      5. Understanding Long-Range Interactions
         1. 实验设计及结果分析
      6. Breaking Down the Failure Cases
   6. References

回到顶部

LSTM

LSTM 结构

一些参数

• 每个时间步 t：
  • 输入向量： x_t
  • 隐藏状态： h_t
  • 细胞状态（Cell State）： c_t
• 与普通 RNN 相比，LSTM 额外维护了细胞状态 c_t ，可长期存储信息。

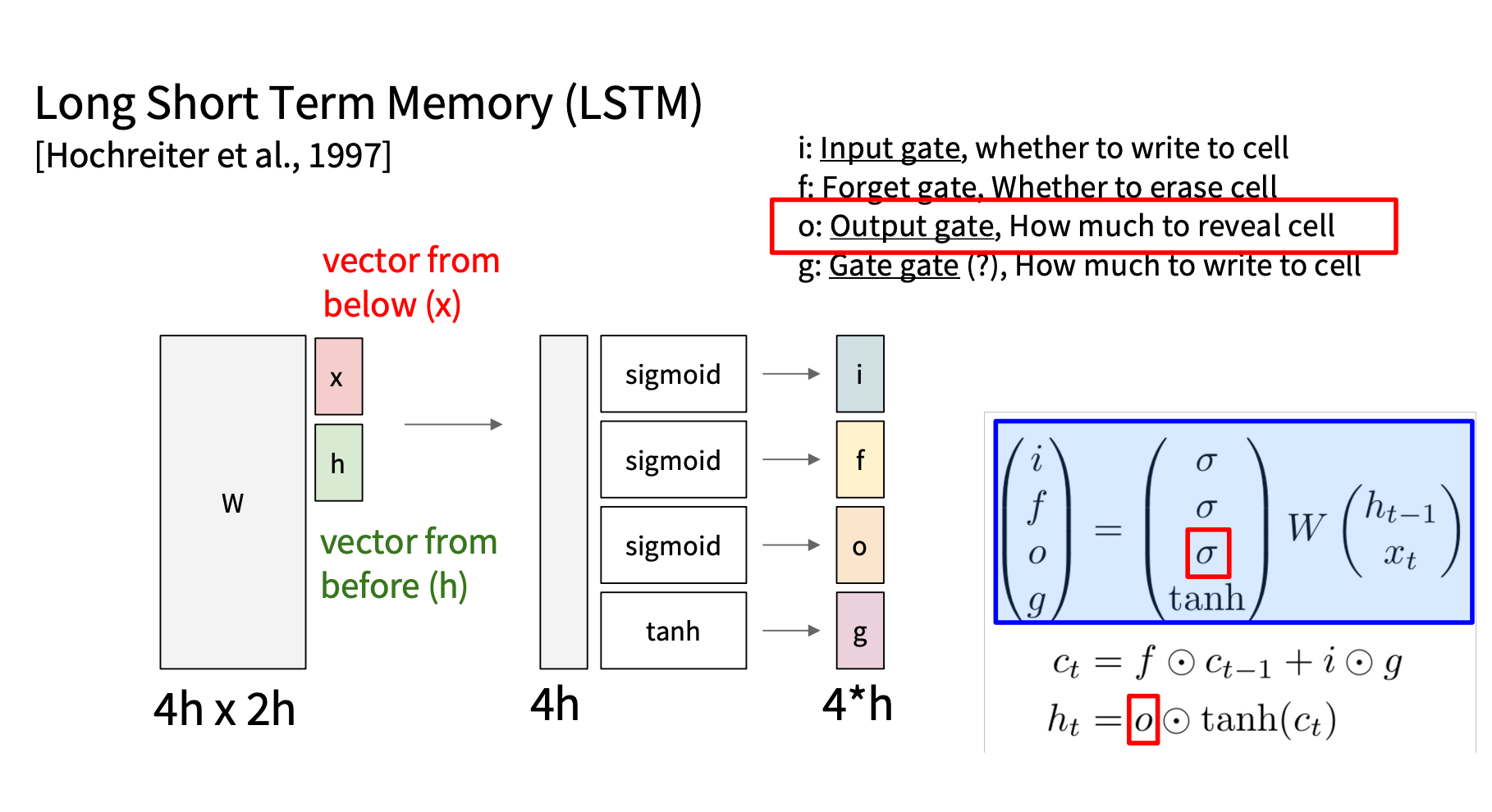
四个门控制机制

image.png

image.png

image.png

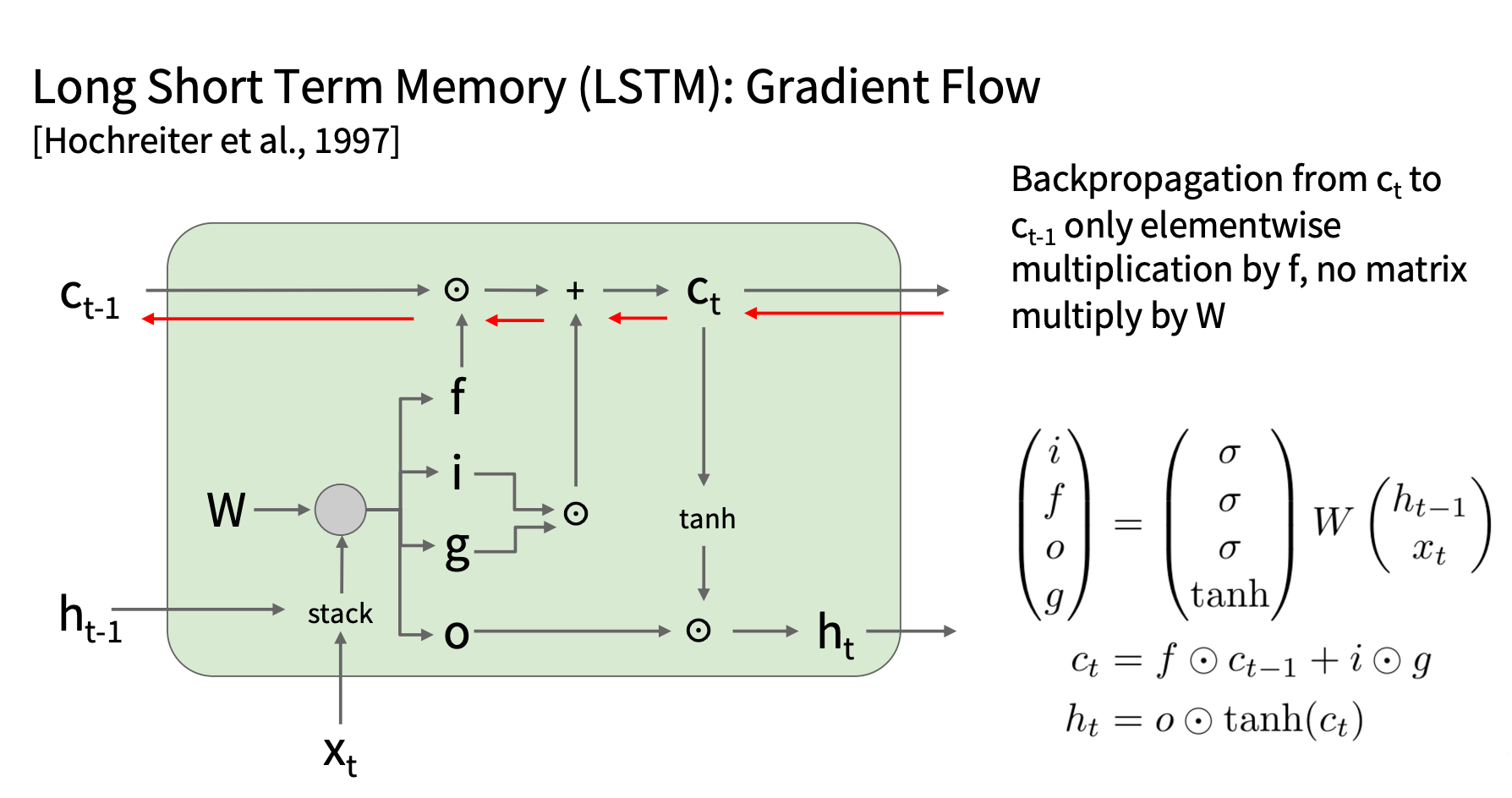
LSTM 通过门控机制控制信息的流动，包括：

门名称	作用	激活函数	数学表达式
遗忘门 ft	控制保留多少旧记忆 ct − 1	sigmoid	ft = σ(Whfht − 1 + Wxfxt)
输入门 it	控制写入多少新信息	sigmoid	it = σ(Whiht − 1 + Wxixt)
候选值 gt	新信息候选值	tanh	gt = tanh (Whght − 1 + Wxgxt)
输出门 ot	控制是否输出当前记忆	sigmoid	ot = σ(Whoht − 1 + Wxoxt)

并行化计算

image.png

3. 细胞状态更新

c_t = f_t ⊙ c_t − 1 + i_t ⊙ g_t

• 过去的信息 c_t − 1 乘以遗忘门 f_t ，决定哪些部分保留。
• 新的信息 g_t 乘以输入门 i_t ，决定哪些部分加入细胞状态。

4. 计算隐藏状态

h_t = o_t ⊙ tanh (c_t)

• 细胞状态 c_t 经过 tanh  变换，使得数值限制在 [-1,1] 之间。
• 乘以输出门 o_t 决定是否输出该信息。

代码演示

注意每一步其实是有多个 cell 并行处理，最后将结果拼接

import torch
import torch.nn as nn

input_size = 10     # one-hot 或 embedding 后的维度
hidden_size = 4     # LSTM 的隐藏层大小 => 有 4 个 Cell
num_layers = 1      # 单层 LSTM

# LSTM
lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_size, num_layers=num_layers)

# 构造输入：1 个时间步，batch_size = 1
# 输入形状：[seq_len, batch_size, input_size]
x = torch.randn(1, 1, input_size)  # 随机模拟一个字符的输入向量

# 初始化隐藏状态和细胞状态
h0 = torch.zeros(num_layers, 1, hidden_size)  # [num_layers, batch_size, hidden_size]
c0 = torch.zeros(num_layers, 1, hidden_size)

# 前向传播
output, (hn, cn) = lstm(x, (h0, c0))

print("输出 output：", output.shape) # torch.Size([1, 1, 4])
print("隐藏状态 hn：", hn.shape) #torch.Size([1, 1, 4])
print("记忆状态 cn：", cn.shape) # torch.Size([1, 1, 4])

---

LSTM 反向传播的优势

用Element-wise Multiplication 的乘法

	矩阵乘法 y = Wx	元素乘法 y = f ⊙ x
计算复杂度	需要 O(n^2) 的计算量	只需要 O(n)
梯度传播	可能导致梯度爆炸或消失（取决于 W 的最大奇异值）	梯度稳定（仅在 0-1 范围内缩放）
数学性质	可能会产生长距离的依赖不稳定	保持梯度方向一致，更稳定

梯度流

image.png

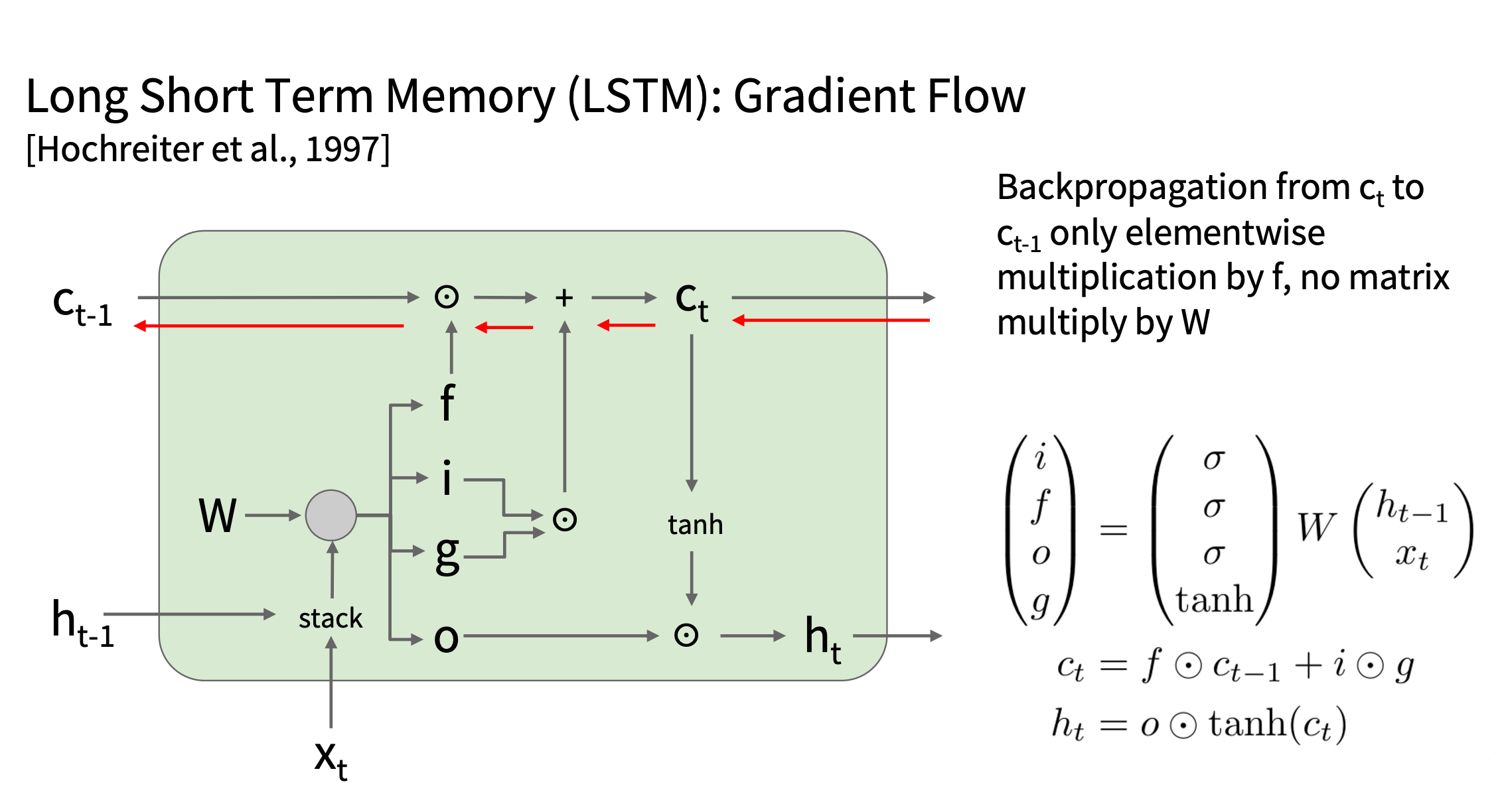
1. 损失 L 首先反向传播到隐藏状态 h_t
2. 再通过 h_t 传递到细胞状态c_t
3. 通过细胞状态 c_t 传递到各个门（输入门 i_t 、遗忘门 f_t 、输出门 o_t 、候选状态 g_t ）
4. 梯度最终回传到 W，因为门的计算公式中包含 W

梯度传播的公式：

由于每个时间步都要计算这个梯度，并进行 累加，时间步数越多，梯度的累积计算就越多。

LSTM 如何用元素乘法解决梯度问题

在 LSTM 中，细胞状态的更新方式是：

c_t = f_t ⊙ c_t − 1 + i_t ⊙ g_t

其中：

• f_t （遗忘门）控制旧信息的保留，其值在 0 到 1 之间。
• i_t （输入门）决定是否加入新信息。

在反向传播时：

LSTM 更稳定原因？

1. LSTM 允许梯度缓慢衰减

• 在 RNN 里，梯度指数级衰减（每一步都乘 W_h 和 1 − tanh²(h_t) ）。
• 在 LSTM 里，梯度只是缓慢乘以 f_t 。

2. 遗忘门f_t 由数据学习

• LSTM 不是固定的f_t ，而是可以学习最优的 f_t 。
• 如果模型检测到需要长期记忆， f_t 会自动接近 1，使得梯度可以长时间传播。
• 在重要的信息上，LSTM 可以动态调整 f_t ，确保梯度不会过早消失。

3. LSTM 允许梯度选择性地消失

• 有些信息应该被遗忘，而有些信息应该长期存储。
• LSTM 通过 f_t 控制哪些信息应该被保留，哪些可以丢弃。
• 这比 RNN 全局性梯度消失/爆炸的情况更合理。

4. 细胞状态不经过 tanh

• 在 RNN 里，梯度在每个时间步都要乘 1 − tanh²(h_t) ，导致指数级衰减。
• 在 LSTM 里，细胞状态梯度传播时不经过 tanh，减少了梯度衰减。

---

LSTM 和ResNet 的相似性

image.png

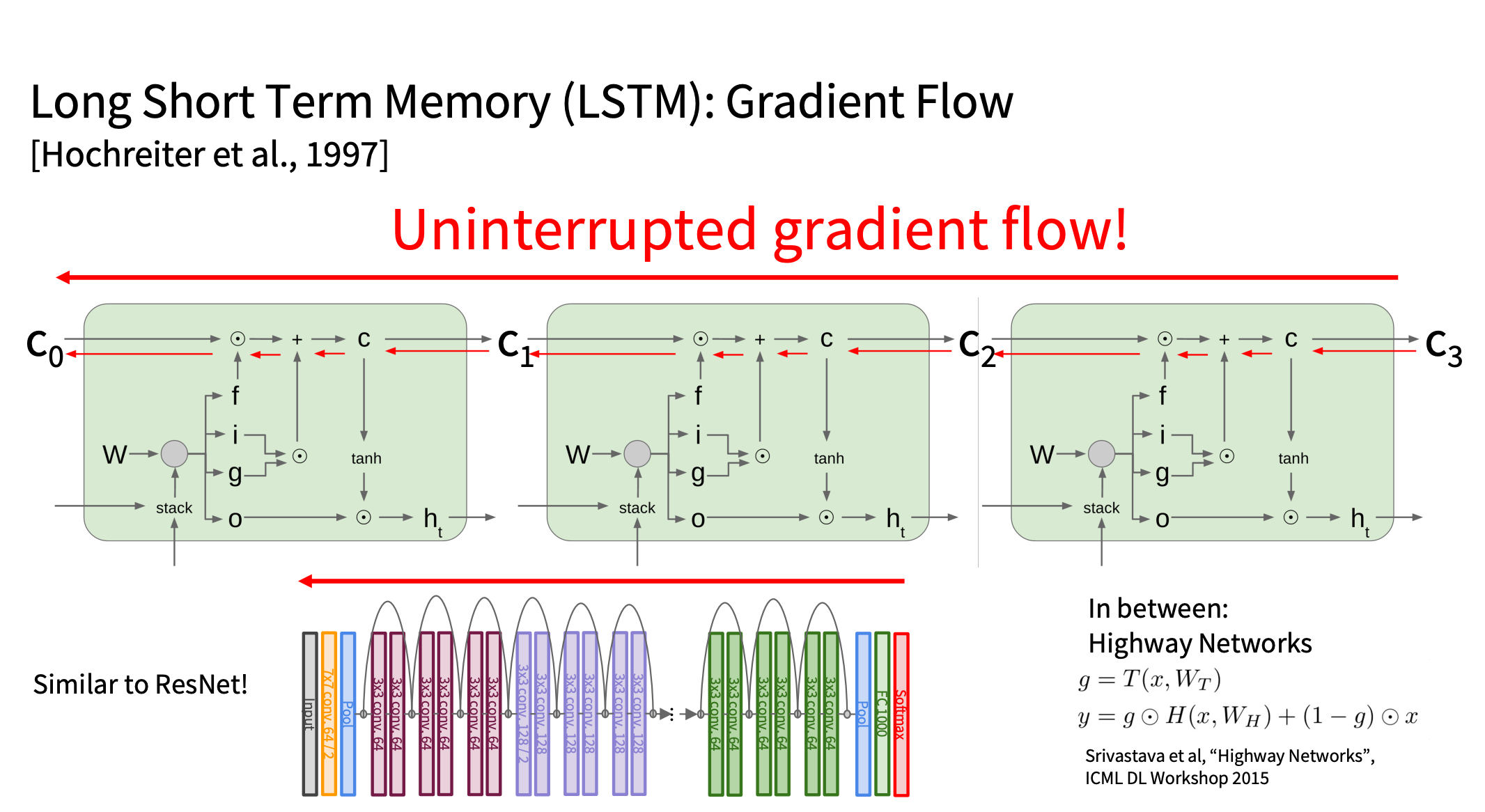
1. LSTM 通过细胞状态 c_t 形成“梯度高速公路”，类似于 ResNet 的残差连接（skip connection）。
2. 高速公路网络（Highway Networks）是介于 LSTM 和 ResNet 之间的一种模型，它结合了门控机制和残差思想。
3. 深度 CNN 和深度 RNN 在训练时面临相似的问题，许多架构设计的灵感可以相互借鉴。

1. LSTM 和 ResNet 的梯度高速公路

在深度网络（无论是 CNN 还是 RNN）中，一个主要挑战是 梯度消失。两种方法都使用了跳跃连接（Skip Connection） 来缓解这个问题：

(1) ResNet 的残差连接

ResNet 解决梯度消失的关键思想是 引入身份连接（Identity Connection）：

y = F(x) + x

其中：

• F(x) 是普通的 CNN 层（例如卷积 + ReLU）。
• 残差连接 + x 确保梯度可以直接从深层传播回前面，不会过度衰减。
• 梯度不会完全依赖于 F(x) 的计算，因此即使 F(x) 计算出一个接近 0 的梯度，x 仍然能保证信息流动。

梯度计算（反向传播）：

这意味着，即使 很小，梯度仍然可以通过 x 直接传播回去，有效缓解了梯度消失问题。

(2) LSTM 的细胞状态

LSTM 也有一个类似的 “身份连接”，即：

c_t = f_t ⊙ c_t − 1 + i_t ⊙ g_t

在反向传播时：

• 类似 ResNet 的跳跃连接，LSTM 允许梯度绕过 tanh  等非线性变换，直接传播到前面的时间步。
• 如果 f_t ≈ 1 ，梯度可以很好地保持，防止梯度消失。
• 这种梯度“高速公路”让 LSTM 在长时间依赖任务上表现比 RNN 好很多。

image.png

• ResNet 通过残差连接确保 CNN 层的梯度可以稳定传播。
• LSTM 通过细胞状态 c_t 提供了一条直接的梯度通道，确保梯度不会完全消失。
• 两者都用到了“梯度高速公路”这一核心思想。

补充: 高速公路网络（Highway Networks)

在 LSTM 和 ResNet 之间，还有一个早期的概念叫 高速公路网络（Highway Networks），它借鉴了 LSTM 的门控机制，并将其应用到 CNN 里。

(1) 高速公路网络的公式

高速公路网络的核心公式：

y = T(x) ⊙ F(x) + (1 − T(x)) ⊙ x

其中：

• F(x) 是普通的神经网络层（例如卷积层）。
• T(x) 是一个门控机制（通常是 sigmoid 函数），决定当前层的输出应该来自于 F(x) 还是直接跳过并使用 x。

如果 T(x) = 1，则：

y = F(x)

如果 T(x) = 0，则：

y = x

这意味着：

• 如果网络需要保留原始信息，就可以让 T(x) 变小，相当于一个跳跃连接。
• 如果网络需要计算更复杂的特征，就让 T(x) 变大，使 F(x) 生效。

梯度计算：

• 这意味着，即使 F(x) 计算出的梯度很小，梯度仍然可以通过 x 直接回传，减少梯度消失问题。

高速公路网络

• 结合了 LSTM 的门控机制（T(x)）和 ResNet 的跳跃连接（+ x）。

• 允许网络动态决定是否应该让信息直接传播，或者应该进行更复杂的计算。

• 高速公路网络的思想后来被用于 ResNet，成为深度 CNN 的关键技术。

架构	关键思想	梯度如何传播？
RNN	隐藏状态 ht 通过 Wh 传播	梯度容易消失（因为每步乘 Wh 和 tanh ）
LSTM	细胞状态 ct 提供梯度高速公路	梯度不会指数级消失（因为 ct 主要通过 ft 传播）
ResNet	残差连接 y = F(x) + x	梯度可以直接传播回前层，不会衰减
Highway Networks	门控连接 y = T(x) ⊙ F(x) + (1 − T(x)) ⊙ x	结合 LSTM 门控机制 + ResNet 的跳跃连接

RNN 可解释性研究

原始论文[1506.02078] Visualizing and Understanding Recurrent Networks

image.png

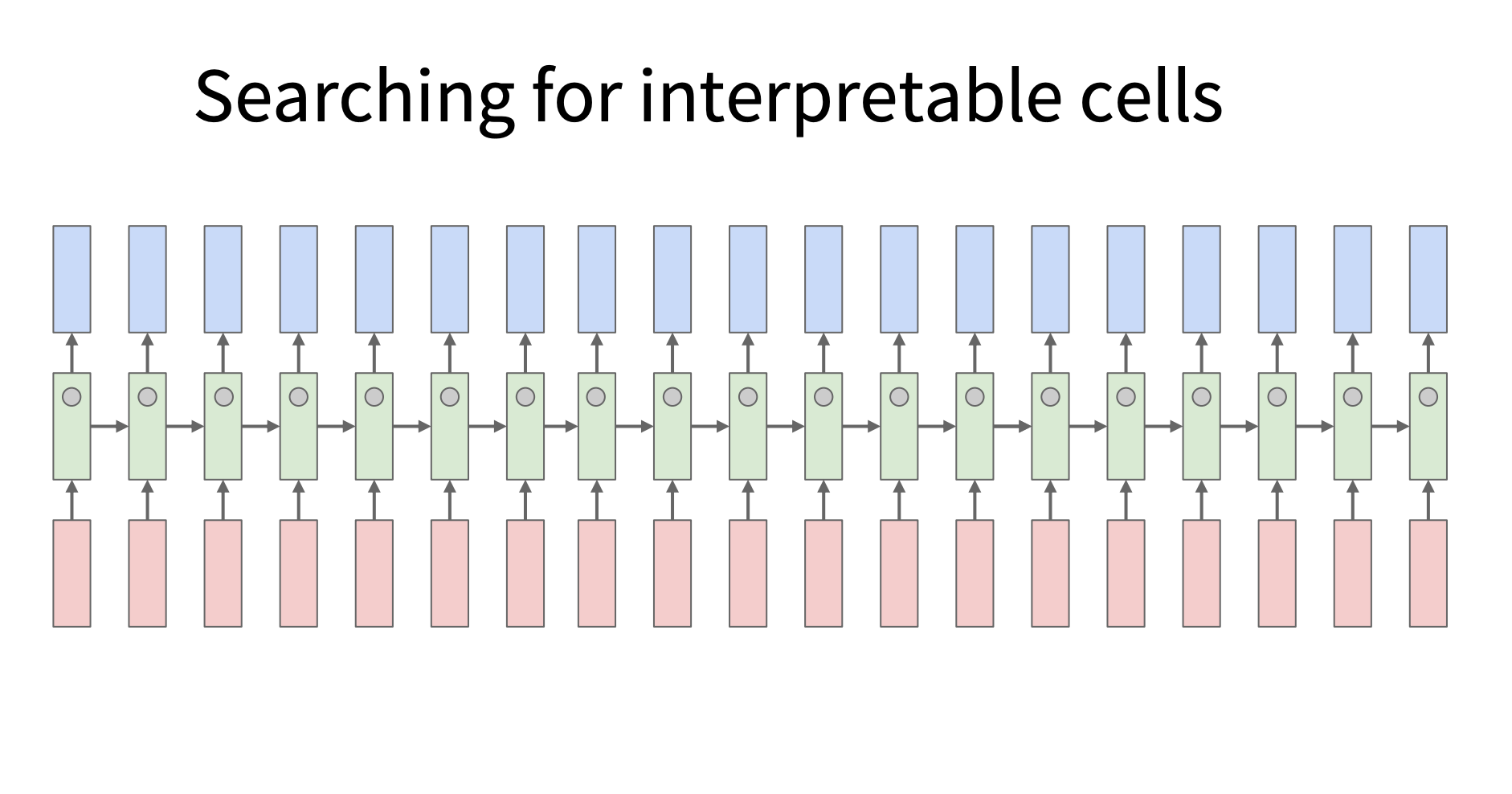
背景 : RNN 内部工作机制难以解释

RNN 通过隐藏状态向量(hidden state vector)存储序列信息，每个时间步都会更新隐藏状态。这些向量中的每个元素(cell)可能在学习过程中捕捉到不同的信息。但RNN 的隐藏状态是一个高维向量，通常难以解释: - 大多数隐藏状态的变化看起来像“随机噪声”。 - 但部分单元可能学习到了有意义的模式，比如识别引号、计算行长度、跟踪代码结构等。

实验设计

1. 分了三组相互对照组: VanillaRNN, LSTM，GRU
2. 字符级语言模型建模: 方便对神经元进行分析
3. 数据集: 战争与和平纯语言数据集以及 Linux 内核源码以测试在不同结构性文本的范化及长建模能

三组比较

1. 从交叉熵损失来看，LSTM 和 GRU 由于RNN

image.png

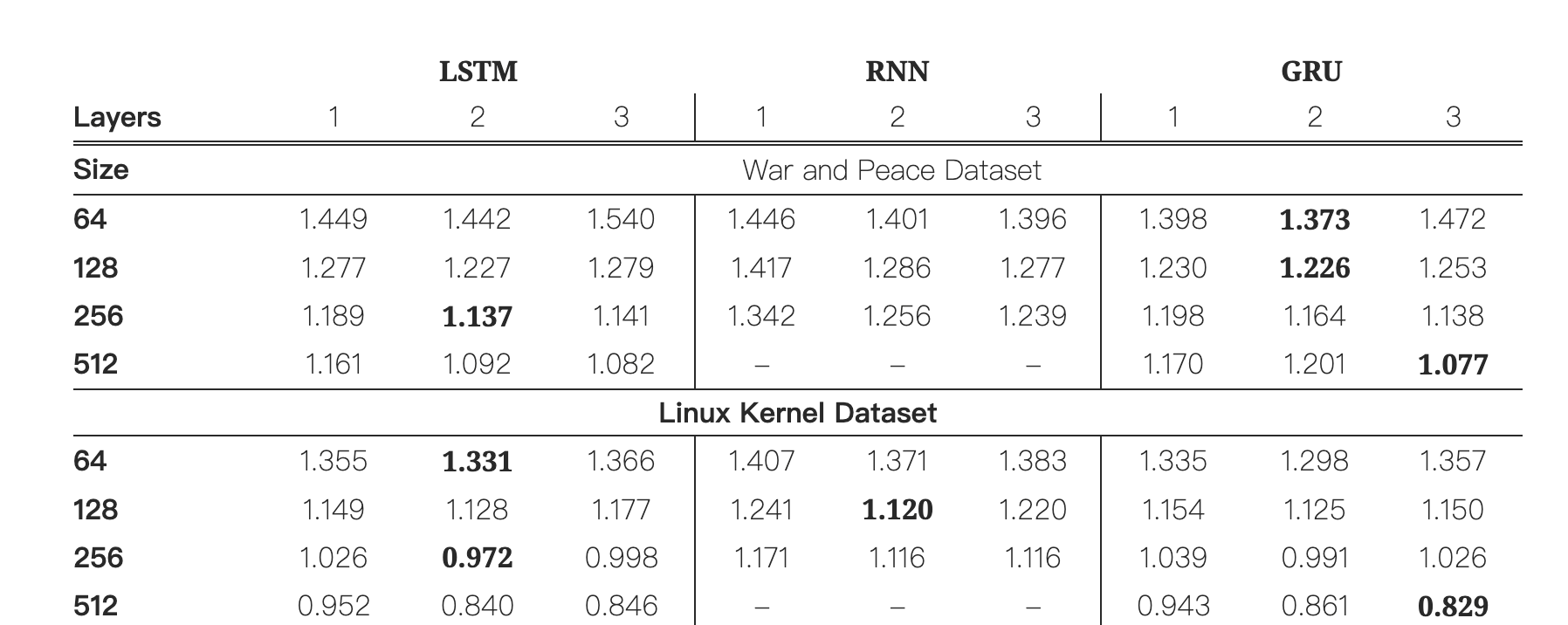
2. 从 t-SNE 可视化来看：LSTM 和 GRU 聚在了一起，说明预测模式相似。而 RNN 则形成相对独立的簇。

image.png

LSTM 内部原理可视化

可解释的长距离 LSTM 单元 (Interpretable, long-range LSTM cells)

1. 利用字符级语言模型的优势，每个时间步每输入一个字符，LSTM 都会更新内部状态，便于观察神经元响应 (准确说是选择每个时间步可解释 cell 来分析)
2. 字符粒度细，可以精准捕捉语法、结构等细节依赖关系。
3. 遍历了所有 Cell 的激活情况，在大量 Cell 中挑选出那些表现出“明显模式”的 Cell 来进行展示。

image.png

Figure 2:Several examples of cells with interpretable activations discovered in our best Linux Kernel and War and Peace LSTMs. Text color corresponds to t​a​n​h​(c), where -1 is red and +1 is blue.

门控激活统计分析(Gate Activation Statistics)

1. 将激活值分为左饱和(<0.1)及右饱和 (>0.9)
2. 分 layer可视化所有 gate (注意梳理层级关系：一个 LSTM 网络可有若干层，每一层为一个完整的 LSTM 结构，每一个 LSTM 结构有很多 cell, 由hidden_size 决定，每一个时间步输入会输入到每一层的所有 Cell 中，所有 Cell 同时更新状态和门控)
3. N 个时间步 × M 个 Cell × 各种 Gate中会产生海量的动态行为, 统计的是比例, 即对每个 Cell 的某个 Gate，计算在所有时间步中，有多少比例时间是 Left Saturated，有多少比例时间是 Right Saturated。

image.png

image.png

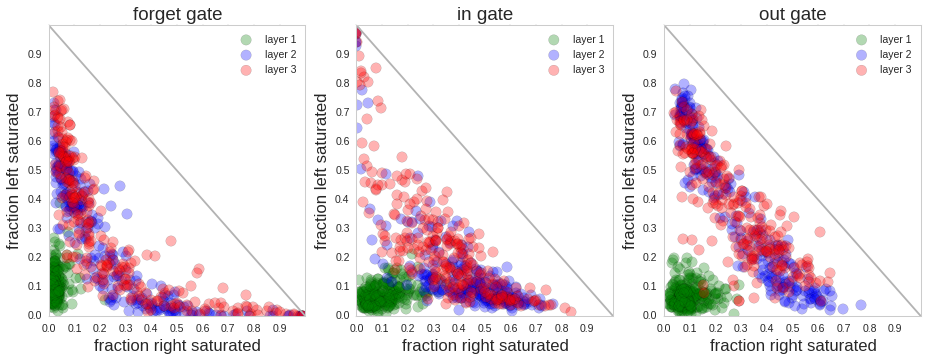
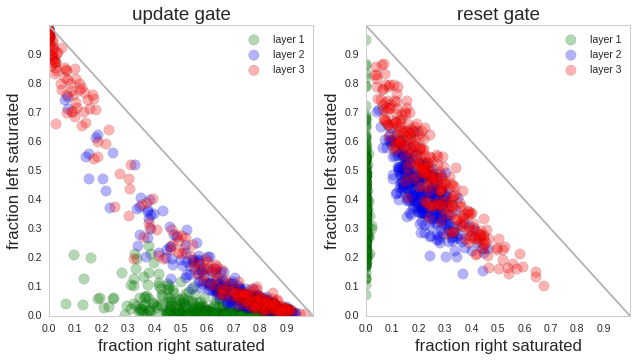
Figure 3: Left three: Saturation plots for an LSTM. Each circle is a gate in the LSTM and its position is determined by the fraction of time it is left or right-saturated. These fractions must add to at most one (indicated by the diagonal line). Right two: Saturation plot for a 3-layer GRU model.

结果分析

• 如果一个点接近右下角：说明这个 Cell 的 Gate 经常完全打开。
• 如果一个点接近左上角：说明这个 Gate 经常完全关闭。
• 如果点分布在中间：说明这个 Gate 经常处于动态调节状态。
• 比如第一层的 gate 经常分布在右下角，则既不常开，也不常关，更多是在做灵活的特征处理，像前馈网络一样动态响应输入。
• Forget Gate很多点集中在右下角，说明部分 Cell 长时间保持记忆（不遗忘）。
• Input Gate & Output Gate：分布更分散，说明输入和输出是动态调节的。
• Update Gate：高层（红色）经常接近饱和，说明更新机制趋向二元化（要么更新，要么保持）。

Understanding Long-Range Interactions

这里想要验证假设: Good performance of LSTMs is frequently attributed to their ability to store long-range information

实验设计及结果分析

1. 对比 LSTM, n-NN(n-gram Neural Network) 和 n-gram 语言模型

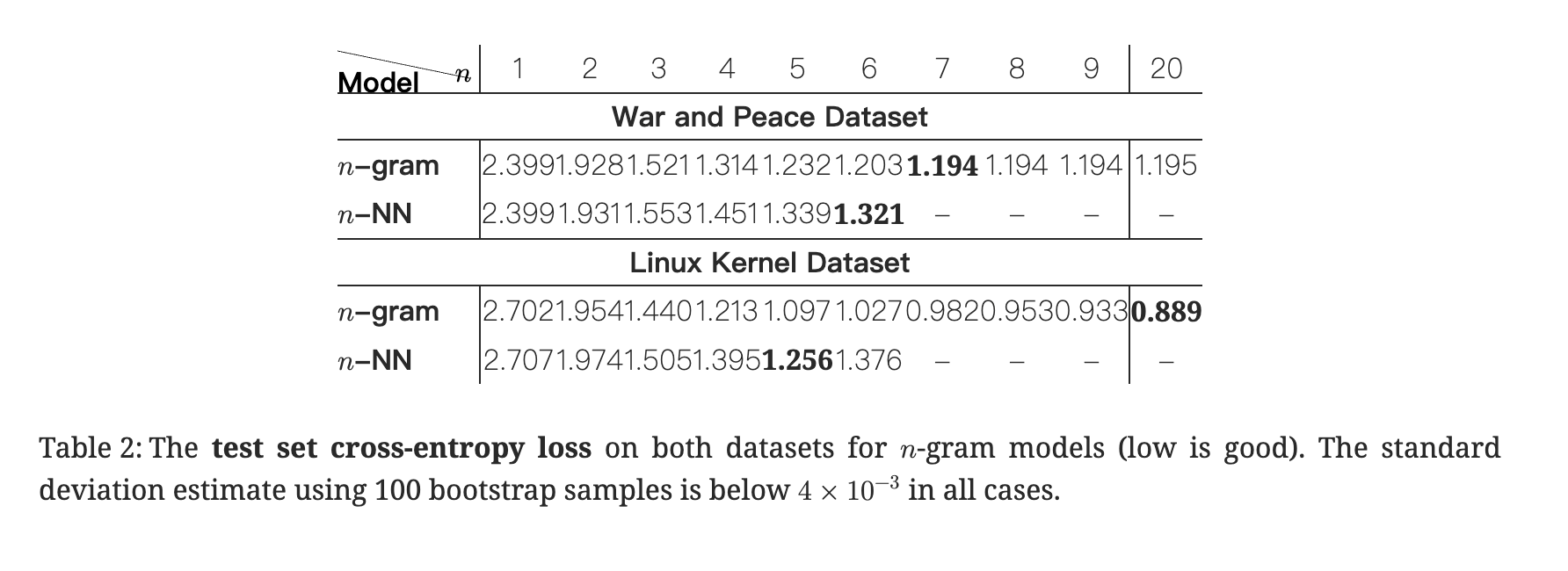这里显示小 n 时（n=1~3），n-gram 和 n-NN 表现接近。随着 n 增大：n-gram 模型效果更好，因为统计模型善于记忆短期模式。n-NN 容易过拟合，性能下降。

image.png

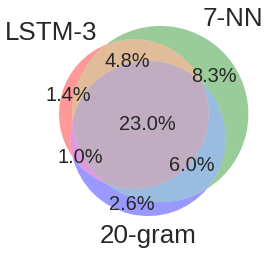
这里显示错误重叠的韦恩图: 对比 LSTM-3、7-NN 和 20-gram 模型在测试集上的错误重叠情况。中间 23%：三者都错的部分。说明不同模型在不同类型的错误上表现不同，LSTM 能避免一些特定错误。这三个模型共享大部分错误率，但每个模型也都有自己独特的错误率

image.png

image.png

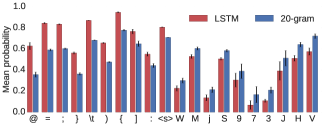
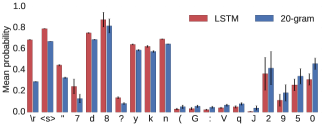
这里显示字符级别的正确率对比: 纵轴：模型给正确字符分配的平均概率。结果：LSTM 在需要长距离推理的特殊字符上表现明显优于 20-gram，比如：空格 、括号、引号、缩进符号、特殊标点等。这些字符往往依赖于上下文的结构性。

image.png

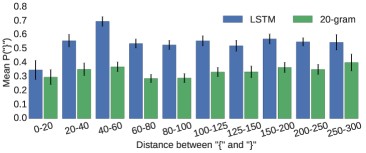
当距离 ≤ 20 时：LSTM 和 20-gram 差距不大（因为 20-gram 刚好还能“看到”开括号）。 当距离 > 20 后：20-gram 性能基本不变，处于“盲猜”水平，因为它看不到对应的开括号。LSTM 表现明显优于 20-gram，说明它能“记住”更远处的开括号信息。 随着距离进一步拉长，LSTM 的优势逐渐减弱，毕竟模型的记忆能力也有限。

image.png

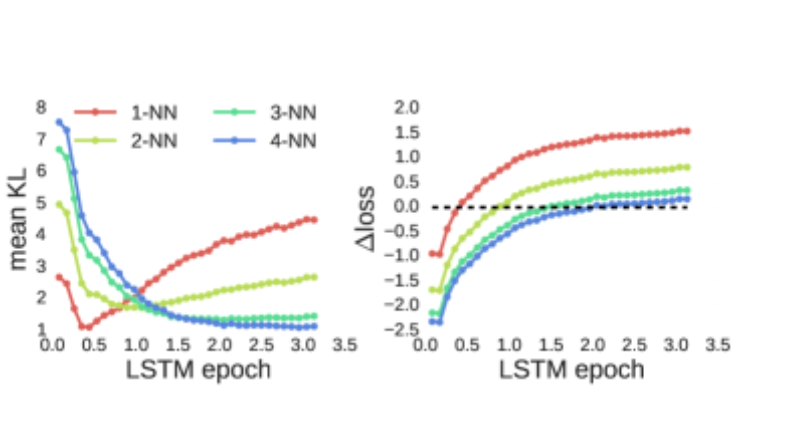
这里绘制 KL散度和平均损失的差异 最初几次迭代中，LSTM 的行为类似于 1-NN 模型，但随后不久就与之偏离。然后，LSTM 的行为依次更像 2-NN、3-NN 和 4-NN 模型。该实验表明，在训练过程中，LSTM 会“增强”其对越来越长的依赖关系的能力

Breaking Down the Failure Cases

这里分类了 LSTM 多错误

image.png

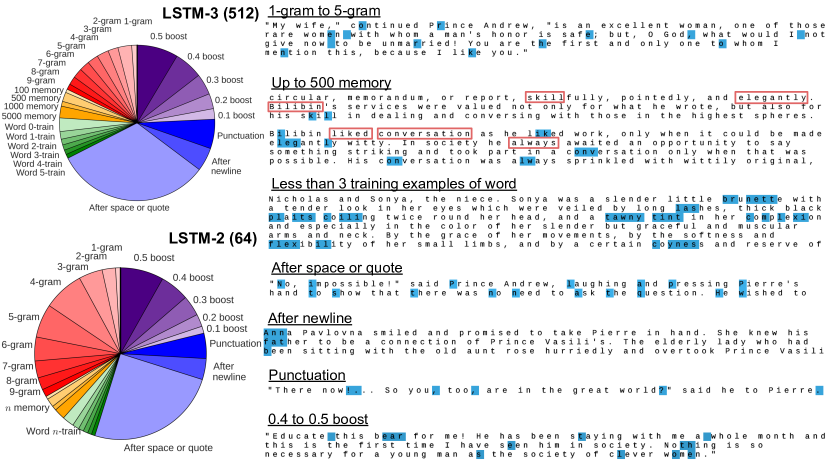
这里显示大模型错误更少，n-gram 类错误占比大；小模型错误更多，boost （无明显特征的残余错误）部分比例明显 但仅仅通过简单堆参数，只能改变 n-gram 类的问题，深层次的错误几乎不受影响，所以需要从架构上进行创新

References

• Understanding LSTMs by Colah
• Visualizing and Understanding Recurrent Networks
• CS231n